Chapter 4 Introduction to Trigonometry

Reading Materials: Croft, A. and R. Davidson Foundation maths. (Harlow: Pearson, 2016) 6th edition. Chapter 22 Introduction to trigonometry.

4.1 Angles

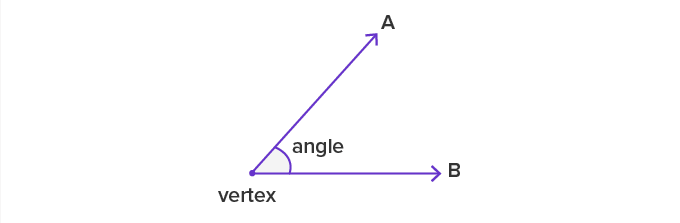
An angle is the measure of separation between two rays that share a common starting point (vertex).

4.1.1 Units of Measurement

• Degrees (°):

  • 1 flat angle = 180°
  • 1 complete angle = 360°
  • 1° = 60 minutes (′)
  • 1′ = 60 seconds (″)

• Radians:

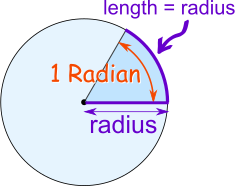
• Defined using the arc of a circle:

  \[\begin{equation} 1 \text{ radian} = \frac{\text{arc length}}{\text{radius}} \end{equation}\]

• A complete circle = \(2\pi\) radians = 360°

• Conversion formulas:

  \[\begin{equation} \text{radians} = \text{degrees} \times \frac{\pi}{180}, \quad \text{degrees} = \text{radians} \times \frac{180}{\pi} \end{equation}\]

4.1.2 Type of Angles

Type of Angle	Measure (Degrees)	Measure (Radians)	Notes
Acute angle	\(0^\circ < \theta < 90^\circ\)	\(0 < \theta < \tfrac{\pi}{2}\)	Smaller than a right angle
Right angle	\(\theta = 90^\circ\)	\(\theta = \tfrac{\pi}{2}\)	Quarter turn
Obtuse angle	\(90^\circ < \theta < 180^\circ\)	\(\tfrac{\pi}{2} < \theta < \pi\)	Between right and flat
Flat angle	\(\theta = 180^\circ\)	\(\theta = \pi\)	Straight line
Reflex angle	\(180^\circ < \theta < 360^\circ\)	\(\pi < \theta < 2\pi\)	More than flat, less than full turn
Complete angle	\(\theta = 360^\circ\)	\(\theta = 2\pi\)	Same as \(0^\circ\) due to periodicity

4.2 Triangles

Definition

• A triangle is a polygon with three sides and three angles.

• The sum of the interior angles of a triangle is always:

  \[\begin{equation} 180^\circ \; \; \text{(or } \pi \text{ radians)} \end{equation}\]

Classification by Sides

• Equilateral: 3 equal sides, 3 equal angles (each 60°).
• Isosceles: 2 equal sides, 2 equal angles.
• Scalene: no equal sides, no equal angles.

Classification by Angles

• Acute triangle: all angles < 90°.
• Right triangle: one angle = 90°.
• Obtuse triangle: one angle > 90°.

Exterior Angle Theorem

• An exterior angle of a triangle equals the sum of the two opposite interior angles:

  \[\begin{equation} \text{Exterior angle} = \text{Angle}_1 + \text{Angle}_2 \end{equation}\]

Triangle Inequality

For any triangle with sides \(a, b, c\):

\[\begin{equation} a + b > c, \quad b + c > a, \quad c + a > b \end{equation}\]

• The sum of the lengths of any two sides must be greater than the third side.
• This condition ensures the three sides can actually form a triangle.

Special case:

• If \(a + b = c\), the points are collinear (they lie on a straight line), so no triangle is formed.

4.2.1 Special Triangles

1. Equilateral Triangle

• All sides are equal: \(a = b = c\)

• All angles are equal: \(60^\circ\) each

• Height formula:

  \[\begin{equation} h = \frac{\sqrt{3}}{2}a \end{equation}\]

• Area:

  \[\begin{equation} A = \frac{\sqrt{3}}{4}a^2 \end{equation}\]

2. Isosceles Triangle

• Two equal sides: \(a = b \neq c\)

• Two equal base angles.

• If base = \(c\), height from apex bisects base:

  \[\begin{equation} h = \sqrt{a^2 - \left(\frac{c}{2}\right)^2} \end{equation}\]

3. Right Triangle

• One angle = \(90^\circ\).

• Sides:

  • Hypotenuse = longest side (opposite right angle).
  • Legs = other two sides.

• Area:

  \[\begin{equation} A = \frac{1}{2} \times \text{(base)} \times \text{(height)} \end{equation}\]

• Foundation for Pythagoras’ Theorem (next section).

4.2.2 Similar Triangles

Definition

Two triangles are similar if they have the same shape but not necessarily the same size.

• Corresponding angles are equal.
• Corresponding sides are proportional.

Notation

\[\begin{equation} \triangle ABC \sim \triangle DEF \end{equation}\]

means \(\angle A = \angle D, \; \angle B = \angle E, \; \angle C = \angle F\) and

\[\begin{equation} \frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} \end{equation}\]

Conditions for Similarity

Two triangles are similar if:

1. AA (Angle-Angle): Two pairs of angles are equal.
2. SSS (Side-Side-Side): Ratios of all three pairs of sides are equal.
3. SAS (Side-Angle-Side): Ratios of two sides are equal and the included angle is equal.

Property

• Ratio of areas of two similar triangles equals the square of the ratio of corresponding sides:

\[\begin{equation} \frac{\text{Area}_1}{\text{Area}_2} = \left(\frac{\text{Side}_1}{\text{Side}_2}\right)^2 \end{equation}\]

4.2.3 Pythagoras’ Theorem

Statement

In a right-angled triangle:

\[\begin{equation} a^2 + b^2 = c^2 \end{equation}\]

• \(a, b\) = legs (sides adjacent to right angle)
• \(c\) = hypotenuse (side opposite the right angle, longest side)

Pythagorean Triples

• Integer solutions to \(a^2 + b^2 = c^2\).

• Common examples:

  • (3, 4, 5)
  • (5, 12, 13)
  • (8, 15, 17)

• Multiples also work (e.g., 6, 8, 10).

4.3 Trigonometric Relations

4.3.1 Basic Ratios (Right Triangles)

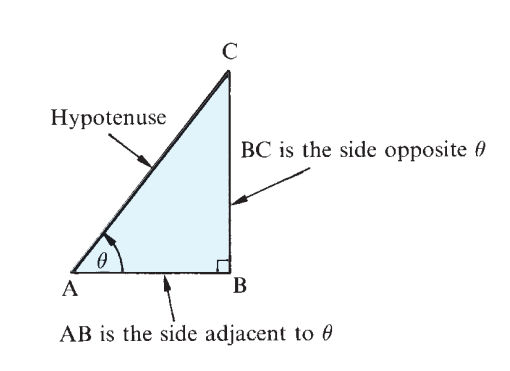
For a right triangle with:

• Angle \(\theta\)
• Opposite side = \(O\)
• Adjacent side = \(A\)
• Hypotenuse = \(H\)

\[\begin{equation} \sin \theta = \frac{O}{H}, \quad \cos \theta = \frac{A}{H}, \quad \tan \theta = \frac{O}{A} \end{equation}\]

Mnemonic: SOH-CAH-TOA

• Sine = Opposite / Hypotenuse
• Cosine = Adjacent / Hypotenuse
• Tangent = Opposite / Adjacent

4.3.2 Law of Sines

\[\begin{equation} \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} \end{equation}\]

Proof:

Construct the altitude from \(B\).

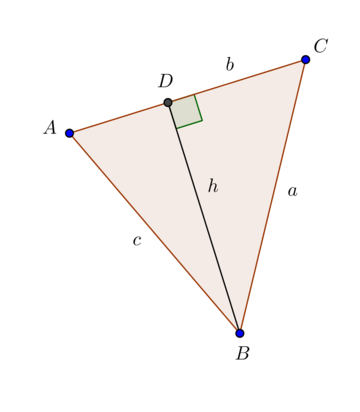
From the definition of sine:

\[\begin{equation} \sin A = \frac{h}{c}, \quad \sin C = \frac{h}{a} \end{equation}\]

Thus:

\[\begin{equation} h = c \sin A, \quad h = a \sin C \end{equation}\]

This gives:

\[\begin{equation} c \sin A = a \sin C \end{equation}\]

So:

\[\begin{equation} \frac{a}{\sin A} = \frac{c}{\sin C} \end{equation}\]

Similarly, constructing the altitude from \(A\) gives:

\[\begin{equation} \frac{b}{\sin B} = \frac{c}{\sin C} \end{equation}\]

4.3.3 Law of Cosines

\[\begin{equation} c^2 = a^2 + b^2 - 2ab\cos C \end{equation}\]

Proof:

Using the same triangle from previous proof, let:

\[\begin{equation} e = \text{CD} \end{equation}\]

\[\begin{equation} f = \text{AD} \end{equation}\]

We have that △CDB and △ADB are right triangles.

Hence:

\[\begin{align} c^2 &= h^2+f^2\\ a^2 &= h^2+e^2\\ b^2 &= (e+f)^2\\ &= e^2+f^2+2ef\\ e &= A \cos C \end{align}\]

Then:

\[\begin{align} c^2 &= h^2+f^2\\ &= a^2-e^2+f^2\\ &= a^2-e^2+f^2+2e^2-2e^2+2ef-2ef\\ &= a^2+\underbrace{(e^2+f^2+2ef)}_{b^2}-2e\underbrace{(e+f)}_b\\ &= a^2 + b^2 - 2ab\cos C \end{align}\]

4.3.4 Special Angles (Summary Table)

Angle	\(\sin \theta\)	\(\cos \theta\)	\(\tan \theta\)
\(0^\circ\)	0	1	0
\(30^\circ\)	\(\tfrac{1}{2}\)	\(\tfrac{\sqrt{3}}{2}\)	\(\tfrac{1}{\sqrt{3}}\)
\(45^\circ\)	\(\tfrac{1}{\sqrt{2}}\)	\(\tfrac{1}{\sqrt{2}}\)	1
\(60^\circ\)	\(\tfrac{\sqrt{3}}{2}\)	\(\tfrac{1}{2}\)	\(\sqrt{3}\)
\(90^\circ\)	1	0	undefined (\(\infty\))